Introduction

When I tell people I study biomedical engineering, they often assume I have a strong background in biology. The truth is, I am terrible at biology, Infact anything to do with ‘memorization’. Interestingly, I found it interesting to study ‘memory’ in the brain, merging the things I hate with something I like. But why should you care about neuroscience and the abstract phenomena biologists’ study with all sorts complicated biology and weird names?

Take AI, the technology that has taken the world by storm. (Sorry to bring it up again, you have probably seen more than enough influencer hype already.) AI is often equated with neural networks. But when AI theorists talk about neural networks, they mean artificial ones. The real neural networks are inside our heads.

This is where mathematical neuroscience comes in. It provides us with a quantitative way to describe how biological neurons behave, converting the complexity of living tissue into mathematical equations. In this post, we will explore some of the most fascinating models of the neural system through a simulation-based lens to look at the natural counterparts of the infamous artificial ones.

Engineering the Neuron

Is the brain like the CPU of a computer? Is the neuron then like a transistor in the brain then? Let’s get to know some properties of the biological neuron, since the brain is primarily an electrical system (a bit of chemical stuff as well) , We would use some ideas for electrical engineering for explaining neuronal behaviour.

The neuron is an electrical unit with the intrinsic ability to generate an action potential once its membrane potential crosses a threshold voltage. As research in the biophysics of neurons progressed, neurophysiologists began exploring how the properties of a neuron could be represented in a computer.

The above neuron model is made using blenderneuron.

Let’s get back to engineering the neuron,the first attempt to do so came in 1943, when Warren McCulloch and Walter Pitts modelled the brain as a computational machine, representing each neuron as a logic gate. Their model reduced a single neuron to a threshold logic unit, expressed by a simple equation. This became the primordial perceptron model, the foundation of modern deep learning:

y=\begin{cases}
1& w^Tx \geq\theta \\
0& w^Tx<\theta
\end{cases}

Here, x represents the input current into the neuron, and w represents synaptic strength.

This equations leans to classify inputs into two classes by learning a separating boundary (something you’d do when you have to separate the good article and bad). While this was a revolutionary step in computer science, it oversimplifies the complex world of biology. The firing representation of a neuron cannot be represented by a zero or a one.

Since neurons can’t be represented as logic gates, researchers sought to understand ion channel dynamics to capture the dynamics of membrane voltage. In 1952, Alan Hodgkin and Andrew Huxley developed a circuit-based mathematical model of the action potentials of the squid giant axon.

Neural Biophysics

The neuron is an electrical system, consisting of charged ions inside and outside of the cell. The charge distribution in the inner and outer regions creates a potential difference. This system of positive and negative charges on the surface of a cell can be modelled as a capacitor, and the input current represents the flow of ions in the cell, giving rise to the fundamendal capacitor equation.

C_{m}\frac{dV}{dt}=\sum I_{ion}

Where cm is the membrane capacitance m; V is the membrane voltage; I represents the current entering the neuron .

To build this model further and understand the membrane potential dynamics, we will assume that the Ion flow for each Ion is governed by the driving potential, defined as the difference between the equilibrium potential from the current cell membrane potential. Moreover, the dynamics of the cell channel are probabilistic, governed by cell membrane dynamics. Considering these dynamics, the Hodgkin–Huxley model can be represented as

\begin{alignat*}{1}

C_m\frac{dV}{dt}&=\bar{g_k}n^4(E_K-V)+\bar{g_{Na}}m^3h(E_{Na}-V)+I_{ext}\\
\frac{dn}{dt}&=\alpha_n(V)(1-n)-\beta_n(V)n\\
\frac{dm}{dt}&=\alpha_m(V)(1-m)-\beta_m(V)m\\
\frac{dh}{dt}&=\alpha_h(V)(1-h)-\beta(V)h
\end{alignat*}

where g represents conductance of ion channel; E represent the equilibrium voltage for a ion; n, m, h represents the fraction of gated being open in a ion channel; The fraction of a channel gate being open is regulated by the channel voltage itself, with the channel gates opening and closing constantly;The power four term in the potassium conductance equation models the fact that four gating variables must simultaneously activate to open the potassium channel and so on.

Researchers noticed something interesting: the m-gate reacts much faster than the others, and the h-gate doesn’t change things all that much. So instead of modeling everything in full detail, we can simplify the system by trimming away the slower or less important parts. That way, we keep the core voltage dynamics intact

\begin{alignat*}{1}
C_m\frac{dV}{dt}&=\bar{g_K}n^4(E_K-V)+\bar{g_{Na}}\cancel{m^3h}(E_{Na}-V)+I_{ext.}\\
\frac{dn}{dt}&=\alpha_n(V)(1-n)-\beta_n(V) n
\end{alignat*}

The voltage dynamics of gates are estimated using data :

\begin{align*}
\alpha_n(V)&=\frac{0.01\left(10-V\right)}{\text{exp}\left(\frac{10-V}{10}\right)-1}\\
\beta_n(V)&=0.125
 \text{ exp}\left(-\frac{V}{80}\right)
\end{align*}

Lets try to simulate this system of non-linear system of equations numerically.

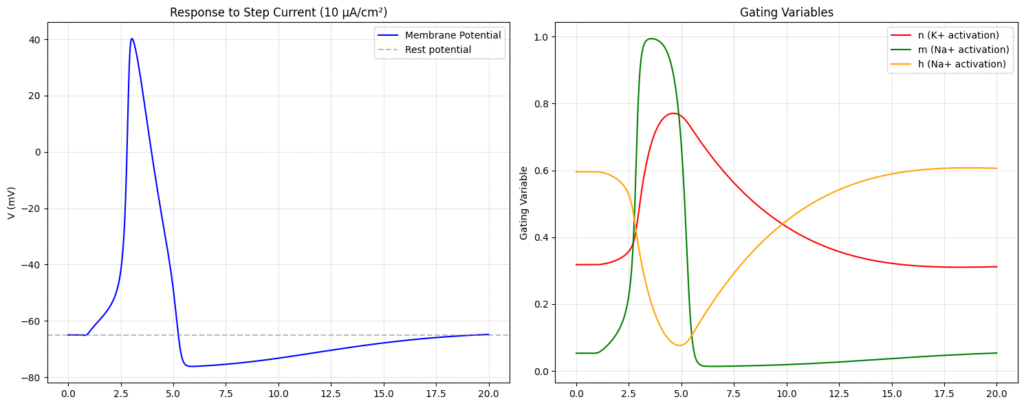
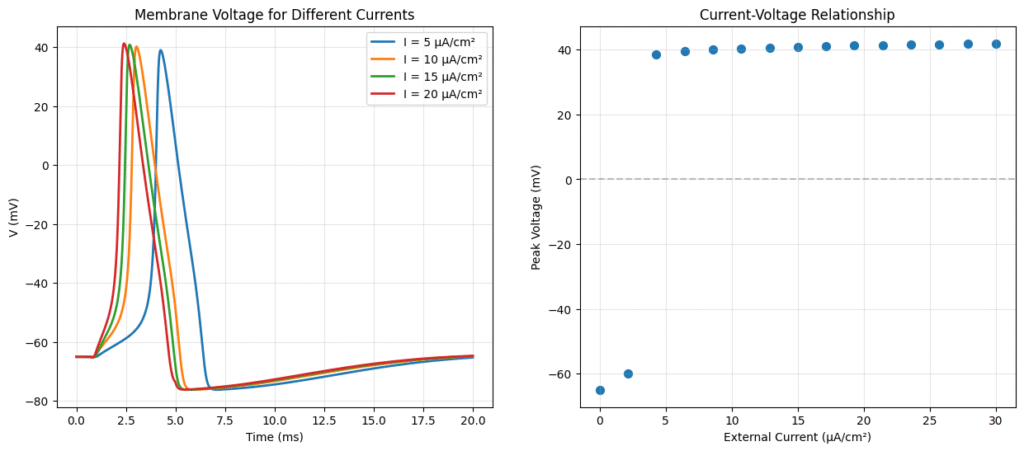
Hence, we say that a neuron fires if the external current entering it, exceeds a threshold

From Biophysics to Dynamics

Well, the numbers and parameters in the Hodgkin-Huxley equation are complicated and non-linear to say the least. Moreover they take a lot of time to run numerically. This time factor is a critical issue if we wish to use bio-inspired models for real life applications.

Fitzhugh and Nagumo reduced the system of Hodgkin–Huxley to two variables and simplified the system of equations for phase plane analysis. We can take a look at some very rich behaviour that can be observed in neurons using this simplified model.

\begin{align*}
\frac{dv}{dt}&=v-\frac{v^3}{3}-w+I_{ext}\\
\frac{dw}{dt}&=\delta(V+a-bw)
\end{align*}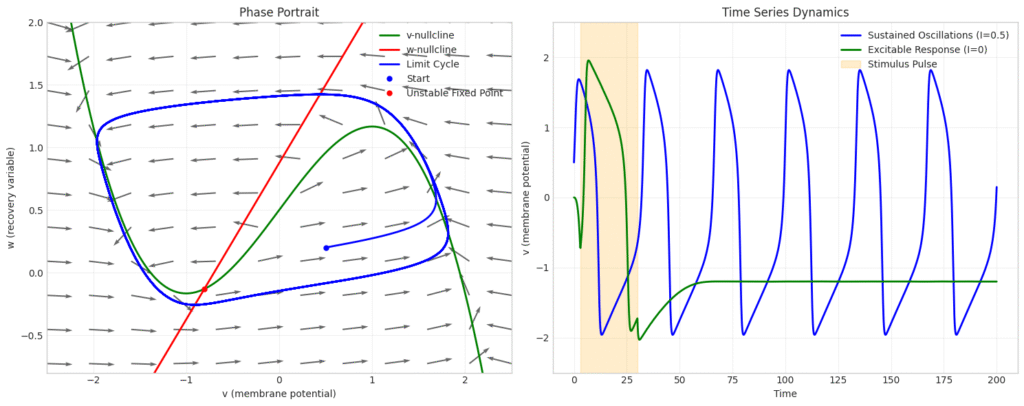

This example shows a sustained oscillatory neuron with a unstable fixed point. What is interesting to observe is that a single neuron may remember the memory of the inputs it received based on the phase at which external current was applied.

This lays the foundation for understanding how even single neurons can contribute to sequence recognition, working memory in the brain

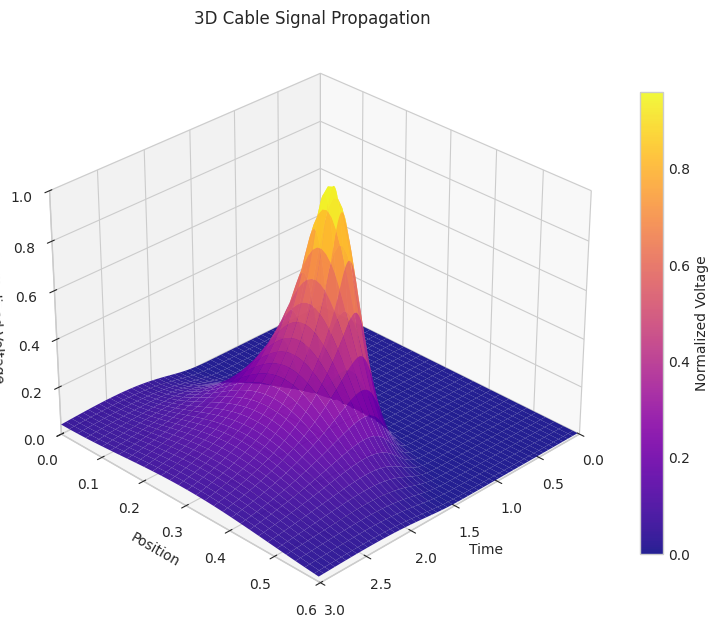
Cable Theory

Realistic neurons are electrically excitable cells where the membrane potential varies not only in time, but also in space. The earlier models we looked at considered the entire neuron as a point dynamic. The cable theory is developed to look at spatio-temporal models of membrane potential dynamics. It considers the axon of the neuron as a charge accumulator, i.e. a capacitor and ion channels act like resistors in parallel.

Applying Kirchhoff’s law on an infinitesimal segment:

\frac{\partial V(x,t)}{\partial t}=\frac{a}{2\rho c_m}\frac{\partial ^2V(x,t)}{\partial x^2}-\frac{g_m}{c_m}V(x,t)- \frac{1}{2\pi a c_m}i_{inj}

The generalised equation can be expressed in the form

\tau_m\frac{\partial V(x,t)}{\partial t}=\lambda^2\frac{\partial ^2V(x,t)}{\partial x^2}-V(x,t)+\frac{1}{2\pi g_m a}i_{inj}

where:

\begin{align*}
\tau_m&=\frac{c_m}{g_m}\\
\lambda^2&=\frac{a}{2\rho c_m}
\end{align*}

where cm is the capacitance; gm is the conductance/length; a is the rod radius; phro is the longitudinal resistivity.

This equation describes how voltage V(x,t) spreads along the axon like dye diffusing through a tube;the decay term shows leakage, and the injection term models any external input current.

Stochastic Neuron Models

We looked at deterministic models for spiking neurons, which can represent single spike cortical recordings pretty well, but thinking about it. Humanity has always created new innovations . In other words human brains have generative capabilites .Generative abilities arise from probabilistic sampling that is experimentally inherent to the behavior of neurons. Here we look at the Galves–Löcherbach model, which provides very interesting spiking visual for neural data modelling.

The probabilty that a neuron spikes at time t

P\left[X_i(t) = 1 \mid \mathcal{F}_{t-1} \right] = \phi_i \left( V_i(t ) \right)

where X represents the firing state of the neuron i.e. 1 or 0; F represents the past input; V represents the synaptic input; phi represents the non-linear activation fucntion;

The total synaptic input for a neuron can be expressed as

V_i(t)=\sum_{j=1}^{N}\sum_{s=t_0}^tw_{ij}(t-s)X(s)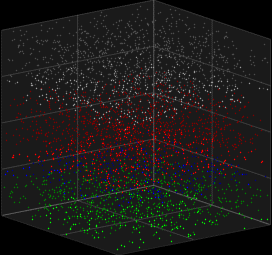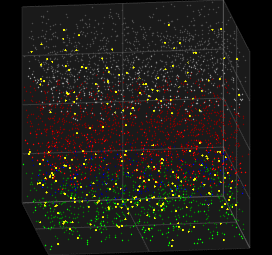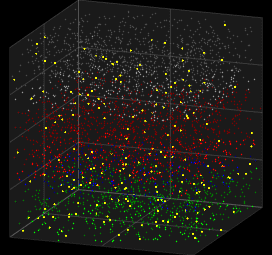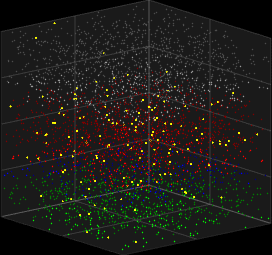

3D Vizualization of the Galves–Löcherbach model; credits wikipedia

Learning in Neurons: Spike Timing-Dependent Plasticity

Imagine if I could take the brain of a person and copy the neurons and synapses on a computer with intricate and realistic equations of each neuron. Can we create a digital human?

We examined some biological neuron models, but realistically, several neurons interact with each other. The collective behaviour of these neurons is what gives rise to the property of intelligence in biology. Here, we look at how network interaction in the spiking neuron system using ‘Hebbian learning’ i.e ‘neurons that fire together, wire together’.

Let us consider a simple case where a pre-synaptic neuron is connected to a post-synaptic neuron, if the pre-synaptic neuron fires before the post synaptic neuron , the strength of synapse between the two neurons increase and vice-versa.

This can be expressed as

\Delta w=
\begin{cases}
A_+e^{\frac{\Delta t}{\tau_+}}(w_{max}-w) \text{ if }t_{pre}\leq t_{post}\\
A_-e^{\frac{\Delta t}{\tau_-}}(w-w_{min}) \text{ if }t_{pre}> t_{post}\\
\end{cases}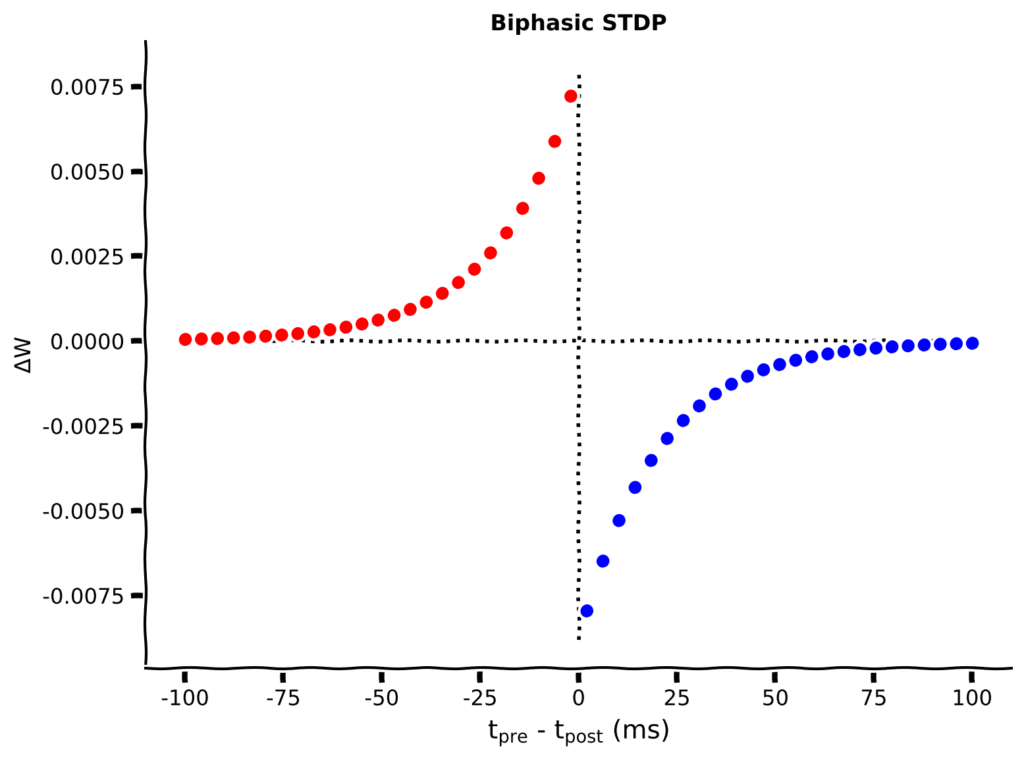

We build a network of neurons with Poisson spike train and observe the weight evolution of the network under this scheme under correlated and uncorrelated spiking methods

A convenient method to keep a track of the spike timings of the neuron is to keep track of the spike memory of the pre and post synaptic neuron

\begin{align*}
\tau_+\dot{x_i}&=-x_i+\sum\delta(t-t_i^k)\\
\tau_-\dot{y_j}&=-y_j +\sum \delta(t-t_j^k)
\end{align*}

On a pre-spike of i:

w_{ij}\leftarrow w_{ij}+\eta A_+e^\frac{{\Delta t}}{\tau_+}(w_{max}-w)y_j

On a post spike of j:

w_{ij} \leftarrow w_{ij}-\eta A_-e^\frac{\Delta t}{\tau_-}(w-w_{min})x_i

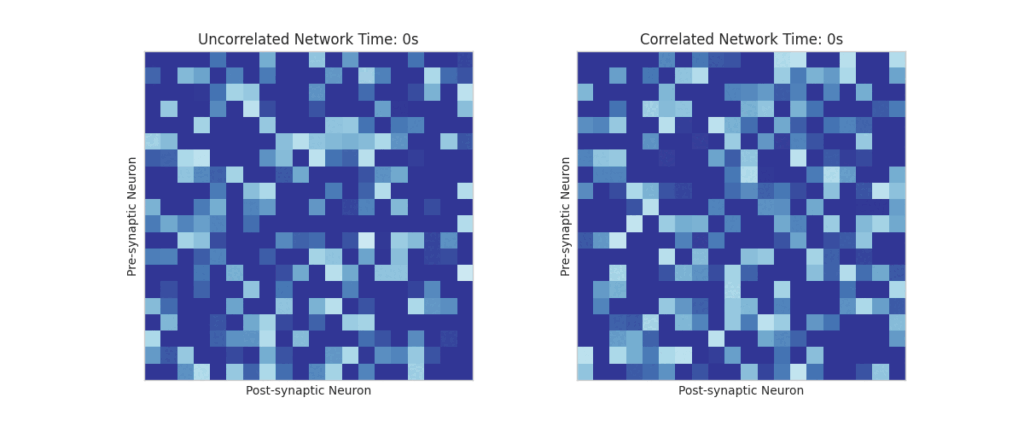
STDP-induced synaptic weight matrices

the introduction of spike-time correlations lead to selective synaptic depression along the bands.

Conclusion

From basic threshold logic units to detailed models of ion channel dynamics and spatially distributed cable theory, we’ve tried to trace the mathematical foundations of how neurons process information. Neuroscientific models provide tools to explore how structure gives rise to function, how networks self-organize, and how biological intelligence emerges from electrical and chemical interactions.

There is still a lot for us to know, and the field of computational neuroscience is ripe for innovations. Humans have explored the earth and the space, possibly it’s time now to explore the organ that drives the urge for human exploration.

Hope you enjoyed reading this article!

References